数据加密的基础知识
0 条参与本文讲解了关于加密相关的基础知识,其中包括对称密钥加密、公钥加密、单向散列算法及其配合使用,对理解HTTPS,SSL/TLS,数字签名等有很大的帮助。
对称密钥加密
对称密钥加密(一个密钥),也叫做共享密钥加密或机密密钥加密,使用发件人和收件人共同拥有的单个密钥。这种密钥既用于加密,也用于解密,叫做机密密钥。对称密钥加密是加密大量数据的一种行之有效的方法。
对称密钥加密有许多种算法如AES,DES,RC4,IDEA等,但所有这些算法都有一个共同的目的:以可还原的方式将明文(未加密的数据)转换为暗文。暗文使用加密密钥编码,对于没有解密密钥的任何人来说它都是没有意义的。由于对称密钥加密在加密和解密时使用相同的密钥,所以这种加密过程的安全性取决于是否有未经授权的人获得了对称密钥。
衡量对称算法优劣的主要尺度是其密钥的长度。密钥越长,在找到解密数据所需的正确密钥之前必须测试的密钥数量就越多。需要测试的密钥越多,破解这种算法就越困难。
公钥加密
公钥加密使用两个密钥:一个公钥和一个私钥,这两个密钥在数学上是相关的。为了与对称密钥加密相对照,公钥加密有时也叫做不对称密钥加密。在公钥加密中,公钥可在通信双方之间公开传递,或在公用储备库中发布,但相关的私钥是保密的。只有使用私钥才能解密用公钥加密的数据。使用私钥加密的数据只能用公钥解密。下图中,发件人拥有收件人的公钥,并用它加密了一封邮件,但只有收件人掌握解密该邮件的有关私钥。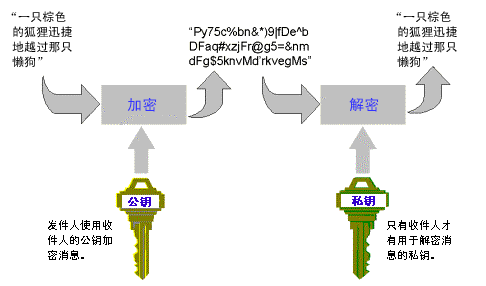
公钥算法的主要局限在于,这种加密形式的速度相对较低。实际上,通常仅在关键时刻才使用公钥算法,如在实体之间交换对称密钥时,或者在签署一封邮件的散列时(散列是通过应用一种单向数学函数获得的一个定长结果,对于数据而言,叫做散列算法)。将公钥加密与其它加密形式(如对称密钥加密)结合使用,可以优化性能,如数字签名和密钥交换。
常用公钥算法:
- RSA:适用于数字签名和密钥交换。 是目前应用最广泛的公钥加密算法,特别适用于通过 Internet 传送的数据,RSA算法以它的三位发明者的名字命名。
- DSA:仅适用于数字签名。 数字签名算法 (Digital Signature Algorithm, DSA) 由美国国家安全署 (United States National Security Agency, NSA) 发明,已作为数字签名的标准。DSA 算法的安全性取决于自计算离散算法的困难。这种算法,不适用于数据加密。
- Diffie-Hellman:仅适用于密钥交换。 Diffie-Hellman 是发明的第一个公钥算法,以其发明者 Whitfield Diffie 和 Martin Hellman 的名字命名。Diffie-Hellman 算法的安全性取决于在一个有限字段中计算离散算法的困难。
单向散列算法
散列,也称为散列值或消息摘要 ,是一种与基于密钥(对称密钥或公钥)的加密不同的数据转换类型。散列就是通过把一个叫做散列算法的单向数学函数应用于数据,将任意长度的一块数据转换为一个定长的、不可逆转的数字,其长度通常在128~256位之间。所产生的散列值的长度应足够长,因此使找到两块具有相同散列值的数据的机会很少。如发件人生成邮件的散列值并加密它,然后将它与邮件本身一起发送。而收件人同时解密邮件和散列值,并由接收到的邮件产生另外一个散列值,然后将两个散列值进行比较。如果两者相同,邮件极有可能在传输期间没有发生任何改变。
下面是几个常用的散列函数:
- MD5:是RSA数据安全公司开发的一种单向散列算法,MD5被广泛使用,可以用来把不同长度的数据块进行暗码运算成一个128位的数值。
- SHA-1:与 DSA 公钥算法相似,安全散列算法1(SHA-1)也是由 NSA 设计的,并由 NIST 将其收录到 FIPS 中,作为散列数据的标准。它可产生一个 160 位的散列值。SHA-1 是流行的用于创建数字签名的单向散列算法。
- MAC(Message Authentication Code):消息认证代码,是一种使用密钥的单向函数,可以用它们在系统上或用户之间认证文件或消息,常见的是HMAC(用于消息认证的密钥散列算法)。
- CRC(Cyclic Redundancy Check):循环冗余校验码,CRC校验由于实现简单,检错能力强,被广泛使用在各种数据校验应用中。占用系统资源少,用软硬件均能实现,是进行数据传输差错检测地一种很好的手段(CRC 并不是严格意义上的散列算法,但它的作用与散列算法大致相同,所以归于此类)。
数字签名:结合使用公钥与散列算法
数字签名是邮件、文件或其它数字编码信息的发件人将他们的身份与信息绑定在一起(即为信息提供签名)的方法。对信息进行数字签名的过程,需要将信息与由发件人掌握的秘密信息一起转换(使用私钥)为叫做签名的标记。数字签名用于公钥环境(任何人都可以拥有)中,它通过验证发件人确实是他或她所声明的那个人,并确认收到的邮件与发送的邮件完全相同。
散列算法处理数据的速度比公钥算法快得多。散列数据还缩短了要签名的数据的长度,因而加快了签名过程。
密钥交换:结合使用对称密钥与公钥
对称密钥算法非常适合于快速并安全地加密数据。但其缺点是,发件人和收件人必须在交换数据之前先交换机密密钥。结合使用加密数据的对称密钥算法与交换机密密钥的公钥算法可产生一种既快速又灵活的解决方案。